TABLE OF CONTENTS (Click to jump) |
Greetings, everyone! Rodrigo here again!
If you're new here, this is the second to last post in a 16-part series where I've broken down everything a musician needs to know, from basic intervals to arpeggios, scales, and major and minor keys. You can easily catch up on the previous posts by clicking their titles below.
I highly recommend reading my articles on major keys, minor keys, harmonic minor keys, and melodic minor keys before diving into this topic. They provide the essential foundation needed to fully understand the concepts covered here about Greek modes. Additionally, while this article focuses on the theoretical aspects of Greek modes, if you're interested in learning how to play them and recognize their unique sound, be sure to check out my article on guitar scales.
To my regular readers, thanks so much for your continued support! As always, I'll keep adding new articles every month, and I'll be updating the store section soon with some cool new stuff. If you haven't already, bookmark this blog and drop a comment below with any topics you'd like me to cover in the future.
Thank you all!
Rodrigo
List of posts:
Simples Intervals -> Compound Intervals -> Triads -> Drop-2 Chords -> Drop-3 Chords -> Shell Chords & Extensions -> Triads & Extensions -> Chord Melody -> Guitar Arpeggios -> Guitar Scales -> Major Keys -> Minor Keys -> Harmonic Minor Keys -> Melodic Minor Keys -> Greek Modes -> Chord Progressions
GREEK MODES
The Greek modes are a series of seven musical scales, each derived from one of the seven degrees (or notes) of the major scale. Each mode has a distinct sequence of intervals, giving it a unique tonal character and mood. These modes include Ionian (starting from the 1st degree), Dorian (2nd degree), Phrygian (3rd degree), Lydian (4th degree), Mixolydian (5th degree), Aeolian (6th degree), and Locrian (7th degree). They are widely used in both ancient and modern music for their varied harmonic and melodic possibilities.
In other words, the Greek modes are the major scale starting from different notes and keeping the same scale structure. I'll break down each one of them and you'll be able to easily understand it:
IONIAN MODE (Major scale's first degree)
Since the Ionian mode starts on the first degree of the major scale, it shares the same formula as the major scale:
whole tone - whole tone - semitone - whole tone - whole tone - whole tone - semitone.
For example, the C Ionian mode (C major scale) follows this exact pattern of notes: C D E F G A B. This mode contains the same sequence of notes and chords (triads and 7th chords) as the major scale. Therefore, the Ionian mode is essentially the major scale and can be represented by the following formula:
1 2 3 4 5 6 7
This represents the root (1), major 2nd (2), major 3rd (3), perfect 4th (4), perfect 5th (5), major 6th (6), and major 7th (7).
The defining characteristic of any mode lies in its first chord. The Ionian mode is known for generating a major 7th chord (root, 3rd, 5th, 7th) and features a perfect 4th. However, while the perfect 4th (extension 11) is characteristic of the Ionian mode, it is generally avoided when playing over a major chord. This is because the 4th can create dissonance with the major 3rd, so it’s best used as a passing note in solos or melodies, rather than being played simultaneously with a major chord.
*The Ionian mode is the only Greek mode that has a major 7th chord in the first degree with a perfect 11th as an extension!
Now that we understand the formula for the Ionian mode, let’s explore the notes and chords generated by the C Ionian mode:
Scale notes: C - D - E - F - G - A - B
Triads: C - Dm - Em - F - G - Am - Bdim
7th chords: Cmaj7 - Dm7 - Em7 - Fmaj7 - G7 - Am7 - Bm7(b5)
Tensions:
Cmaj7 (9, 11*, 13)
Dm7 (9, 11, 13)
Em7 (b9*, 11, b13*)
Fmaj7 (9, #11, 13)
G7 (9, 11*, 13)
Am7 (9, 11, b13*)
Bm7(b5) (b9*, 11, b13*)
(*denotes avoid notes)
DORIAN MODE (Major scale's second degree)
The second Greek mode is the Dorian mode. To find its scale formula, we use the major scale formula but start from the second degree. This gives the Dorian mode the following pattern:
whole tone - semitone - whole tone - whole tone - whole tone - semitone - whole tone.
For example, in the C Dorian mode, the sequence of notes would be C D Eb F G A Bb, and the formula can be represented numerically as:
1 2 b3 4 5 6 b7
This represents the root (1), major 2nd (2), minor 3rd (b3), perfect 4th (4), perfect 5th (5), major 6th (6), and minor 7th (b7). Each number corresponds to the interval between the root and the other six notes in the scale.
The Dorian mode’s defining chord is a minor 7th chord (root, b3th, 5th, b7th), and its characteristic note is the major 6th (extension 13), which distinguishes it from other minor modes.
*The Dorian mode is the only Greek mode that has a minor 7th chord in the first degree with a major 13th as an extension!
Now that we understand the formula for the Dorian mode, let’s explore the notes and chords generated by the C Dorian mode:
Scale notes: C - D - Eb - F - G - A - Bb
Triads: Cm - Dm - Eb - F - Gm - Adim - Bb
7th chords: Cm7 - Dm7 - Ebmaj7 - F7 - Gm7 - Am7(b5) - Bbmaj7
Tensions:
Cm7 (9, 11, 13)
Dm7 (b9*, 11, b13*)
Ebmaj7 (9, #11, 13)
F7 (9, 11*, 13)
Gm7 (9, 11, b13*)
Am7(b5) (b9*, 11, b13*)
Bbmaj7 (9, 11*, 13)
(*denotes avoid notes)
PHRYGIAN MODE (Major scale's third degree)
The third Greek mode is the Phrygian mode. To find its scale formula, we use the major scale formula but start from the third degree. This gives the Phrygian mode the following pattern:
semitone - whole tone - whole tone - whole tone - semitone - whole tone - whole tone.
For example, in the C Phrygian mode, the sequence of notes would be C Db Eb F G Ab Bb, and the formula can be represented numerically as:
1 b2 b3 4 5 b6 b7
This represents the root (1), minor 2nd (b2), minor 3rd (b3), perfect 4th (4), perfect 5th (5), minor 6th (b6), and minor 7th (b7). Each number corresponds to the interval between the root and the other six notes in the scale.
The Phrygian mode’s defining chord is a minor 7th chord (root, b3th, 5th, b7th), and its characteristic note is the minor 2nd (extension b9), which distinguishes it from other minor modes.
*The Phrygian mode is the only Greek mode that has a minor 7th chord in the first degree with a minor 9th as an extension!
Now that we understand the formula for the Phrygian mode, let’s explore the notes and chords generated by the C Phrygian mode:
Scale notes: C - Db - Eb - F - G - Ab - Bb
Triads: Cm - Db - Eb - Fm - Gdim - Ab - Bbm
7th chords: Cm7 - Dbmaj7 - Eb7 - Fm7 - Gm7(b5) - Abmaj7 - Bbm7
Tensions:
Cm7 (b9*, 11, b13*)
Dbmaj7 (9, #11, 13)
Eb7 (9, 11*, 13)
Fm7 (9, 11, b13*)
Gm7(b5) (b9*, 11, b13*)
Abmaj7 (9, 11*, 13)
Bbm7 (9, 11, 13)
(*denotes avoid notes)
LYDIAN MODE (Major scale's fourth degree)
The fourth Greek mode is the Lydian mode. To find its scale formula, we use the major scale formula but start from the fourth degree. This gives the Lydian mode the following pattern:
whole tone - whole tone - whole tone - semitone - whole tone - whole tone - semitone.
For example, in the C Lydian mode, the sequence of notes would be C D E F# G A B, and the formula can be represented numerically as:
1 2 3 #4 5 6 7
This represents the root (1), major 2nd (2), major 3rd (3), augmented 4th (#4), perfect 5th (5), major 6th (6), and major 7th (7). Each number corresponds to the interval between the root and the other six notes in the scale.
The Lydian mode’s defining chord is a major 7th chord (root, 3rd, 5th, 7th), and its characteristic note is the augmented 4th (extension #11), which distinguishes it from other major modes.
*The Lydian mode is the only Greek mode that has a major 7th chord in the first degree with an augmented 11th as an extension!
Now that we understand the formula for the Lydian mode, let’s explore the notes and chords generated by the C Lydian mode:
Scale notes: C - D - E - F# - G - A - B
Triads: C - D - Em - F#dim - G - Am - Bm
7th chords: Cmaj7 - D7 - Em7 - F#m7(b5) - Gmaj7 - Am7 - Bm7
Tensions:
Cmaj7 (9, #11, 13)
D7 (9, 11*, 13)
Em7 (9, 11, b13*)
F#m7(b5) (b9*, 11, b13*)
Gmaj7 (9, 11*, 13)
Am7 (9, 11, 13)
Bm7 (b9*, 11, b13*)
(*denotes avoid notes)
MIXOLYDIAN MODE (Major scale's fifth degree)
The fifth Greek mode is the Mixolydian mode. To find its scale formula, we use the major scale formula but start from the fifth degree. This gives the Mixolydian mode the following pattern:
whole tone - whole tone - semitone - whole tone - whole tone - semitone - whole tone.
For example, in the C Mixolydian mode, the sequence of notes would be C D E F G A Bb, and the formula can be represented numerically as:
1 2 3 4 5 6 b7
This represents the root (1), major 2nd (2), major 3rd (3), perfect 4th (4), perfect 5th (5), major 6th (6), and minor 7th (b7). Each number corresponds to the interval between the root and the other six notes in the scale.
The Mixolydian mode’s defining chord is a dominant 7th chord (root, 3rd, 5th, b7th), and its characteristic note is the perfect 4th (extension 11), which distinguishes it from other major modes.
*The Mixolydian mode is the only Greek mode that has a dominant 7th chord in the first degree with a perfect 11th as an extension!
Now that we understand the formula for the Mixolydian mode, let’s explore the notes and chords generated by the C Mixolydian mode:
Scale notes: C - D - E - F - G - A - Bb
Triads: C - Dm - Edim - F - Gm - Am - Bb
7th chords: C7 - Dm7 - Em7(b5) - Fmaj7 - Gm7 - Am7 - Bbmaj7
Tensions:
C7 (9, 11*, 13)
Dm7 (9, 11, b13*)
Em7(b5) (b9*, 11, b13*)
Fmaj7 (9, 11*, 13)
Gm7 (9, 11, 13)
Am7 (b9*, 11, b13*)
Bbmaj7 (9, #11, 13)
(*denotes avoid notes)
AEOLIAN MODE (Major scale's sixth degree)
The sixth Greek mode is the Aeolian mode. To find its scale formula, we use the major scale formula but start from the sixth degree. This gives the Aeolian mode the following pattern:
whole tone - semitone - whole tone - whole tone - semitone - whole tone - whole tone.
For example, in the C Aeolian mode, the sequence of notes would be C D Eb F G Ab Bb, and the formula can be represented numerically as:
1 2 b3 4 5 b6 b7
This represents the root (1), major 2nd (2), minor 3rd (b3), perfect 4th (4), perfect 5th (5), minor 6th (b6), and minor 7th (b7). Each number corresponds to the interval between the root and the other six notes in the scale.
The Aeolian mode’s defining chord is a minor 7th chord (root, b3rd, 5th, b7th), and its characteristic note is the minor 6th (extension b13), which distinguishes it from other minor modes.
*The Aeolian mode is the only Greek mode that has a minor 7th chord in the first degree with a minor 13th as an extension!
Now that we understand the formula for the Aeolian mode, let’s explore the notes and chords generated by the C Aeolian mode:
Scale notes: C - D - Eb - F - G - Ab - Bb
Triads: Cm - Ddim - Eb - Fm - Gm - Ab - Bb
7th chords: Cm7 - Dm7(b5) - Ebmaj7 - Fm7 - Gm7 - Abmaj7 - Bb7
Tensions:
Cm7 (9, 11, b13*)
Dm7(b5) (b9*, 11, b13*)
Ebmaj7 (9, 11*, 13)
Fm7 (9, 11, 13)
Gm7 (b9*, 11, b13*)
Abmaj7 (9, #11, 13)
Bb7 (9, 11*, 13)
(*denotes avoid notes)
LOCRIAN MODE (Major scale's seventh degree)
The seventh Greek mode is the Locrian mode. To find its scale formula, we use the major scale formula but start from the seventh degree. This gives the Locrian mode the following pattern:
semitone - whole tone - whole tone - semitone - whole tone - whole tone - whole tone.
For example, in the C Locrian mode, the sequence of notes would be C Db Eb F Gb Ab Bb, and the formula can be represented numerically as:
1 b2 b3 4 b5 b6 b7
This represents the root (1), minor 2nd (b2), minor 3rd (b3), perfect 4th (4), diminished 5th (b5), minor 6th (b6), and minor 7th (b7). Each number corresponds to the interval between the root and the other six notes in the scale.
The Locrian mode’s defining chord is a minor 7th (b5) chord (root, b3rd, b5th, b7th), and its characteristic note is the minor 2nd (extension b9), which distinguishes it from other minor modes.
*The Locrian mode is the only Greek mode that has a minor 7th (b5) chord in the first degree with a minor 13th as an extension!
Now that we understand the formula for the Locrian mode, let’s explore the notes and chords generated by the C Locrian mode:
Scale notes: C - Db - Eb - F - Gb - Ab - Bb
Triads: Cdim - Db - Ebm - Fm - Gb - Ab - Bbm
7th chords: Cm7(b5) - Dbmaj7 - Ebm7 - Fm7 - Gbmaj7 - Ab7 - Bbm7
Tensions:
Cm7(b5) (b9*, 11, b13*)
Dbmaj7 (9, 11*, 13)
Ebm7 (9, 11, 13)
Fm7 (b9*, 11, b13*)
Gbmaj7 (9, #11, 13)
Ab7 (9, 11*, 13)
Bbm7 (9, 11, b13*)
(*denotes avoid notes)
CHART OF GREEK MODES |
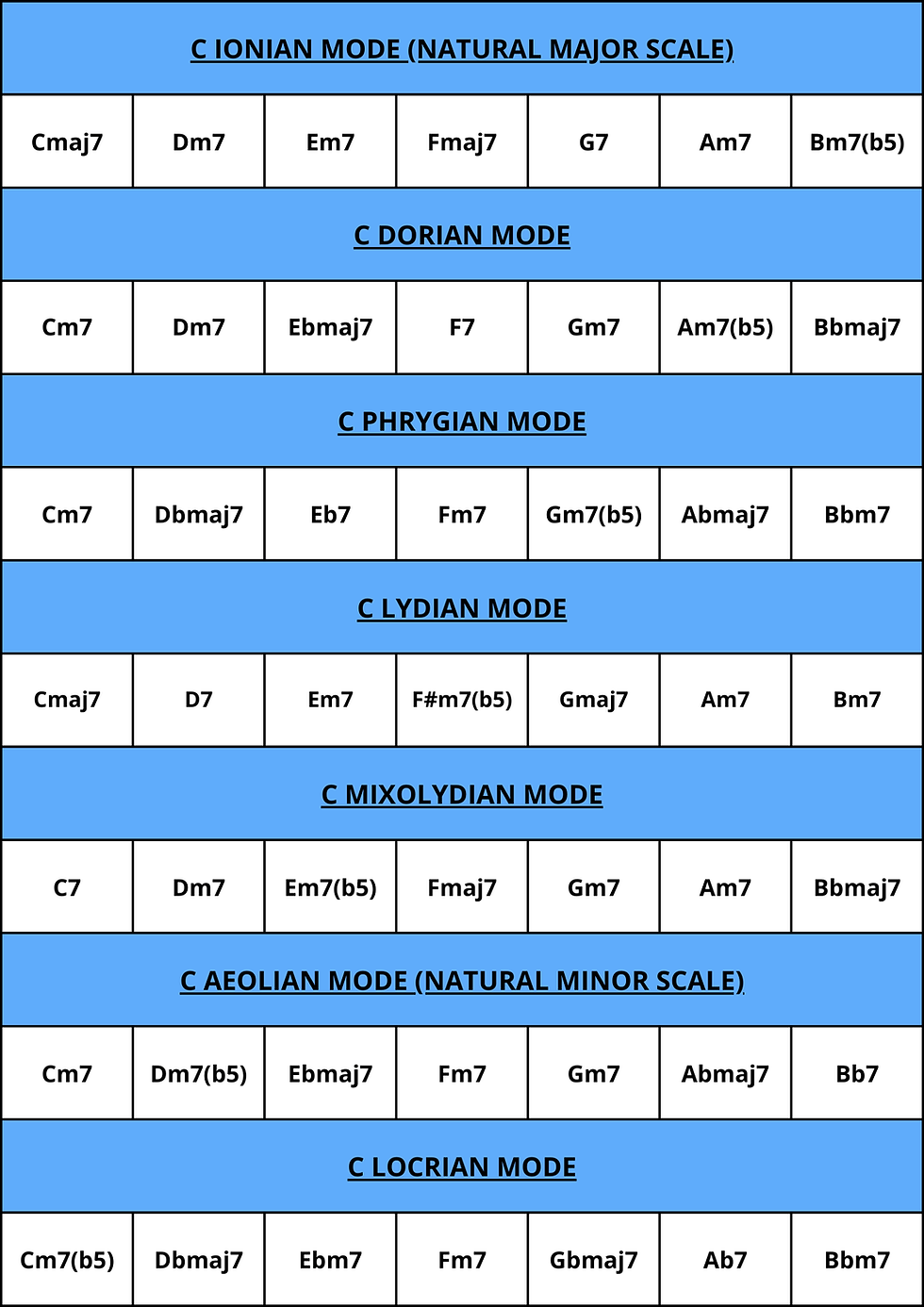
GREEK MODES FROM THE NATURAL MINOR SCALE
As we covered in the article on "Minor Keys", the natural minor scale shares the same pattern as the sixth degree of the major scale. This means the Aeolian mode is equivalent to the natural minor scale. As a result, the other modes remain identical to those of the major scale, but we now treat the Aeolian mode as the first mode in this context.
AEOLIAN MODE (Natural minor scale's first degree)
The first Greek mode of the natural minor scale is the Aeolian mode. To find its scale formula, we use the natural minor scale formula from the first degree or the major scale formula but start from the sixth degree. This gives the Aeolian mode the following pattern:
whole tone - semitone - whole tone - whole tone - semitone - whole tone - whole tone.
For example, in the C Aeolian mode, the sequence of notes would be C D Eb F G Ab Bb, and the formula can be represented numerically as:
1 2 b3 4 5 b6 b7
This represents the root (1), major 2nd (2), minor 3rd (b3), perfect 4th (4), perfect 5th (5), minor 6th (b6), and minor 7th (b7). Each number corresponds to the interval between the root and the other six notes in the scale.
The Aeolian mode’s defining chord is a minor 7th chord (root, b3rd, 5th, b7th), and its characteristic note is the minor 6th (extension b13), which distinguishes it from other minor modes.
*The Aeolian mode is the only Greek mode that has a minor 7th chord in the first degree with a minor 13th as an extension!
Now that we understand the formula for the Aeolian mode, let’s explore the notes and chords generated by the C Aeolian mode:
Scale notes: C - D - Eb - F - G - Ab - Bb
Triads: Cm - Ddim - Eb - Fm - Gm - Ab - Bb
7th chords: Cm7 - Dm7(b5) - Ebmaj7 - Fm7 - Gm7 - Abmaj7 - Bb7
Tensions:
Cm7 (9, 11, b13*)
Dm7(b5) (b9*, 11, b13*)
Ebmaj7 (9, 11*, 13)
Fm7 (9, 11, 13)
Gm7 (b9*, 11, b13*)
Abmaj7 (9, #11, 13)
Bb7 (9, 11*, 13)
(*denotes avoid notes)
LOCRIAN MODE (Natural minor scale's second degree)
The second Greek mode of the natural minor scale is the Locrian mode. To find its scale formula, we use the natural minor scale formula but start from the second degree. This gives the Locrian mode the following pattern:
semitone - whole tone - whole tone - semitone - whole tone - whole tone - whole tone.
For example, in the C Locrian mode, the sequence of notes would be C Db Eb F Gb Ab Bb, and the formula can be represented numerically as:
1 b2 b3 4 b5 b6 b7
This represents the root (1), minor 2nd (b2), minor 3rd (b3), perfect 4th (4), diminished 5th (b5), minor 6th (b6), and minor 7th (b7). Each number corresponds to the interval between the root and the other six notes in the scale.
The Locrian mode’s defining chord is a minor 7th (b5) chord (root, b3rd, b5th, b7th), and its characteristic note is the minor 2nd (extension b9), which distinguishes it from other minor modes.
*The Locrian mode is the only Greek mode that has a minor 7th (b5) chord in the first degree with a minor 13th as an extension!
Now that we understand the formula for the Locrian mode, let’s explore the notes and chords generated by the C Locrian mode:
Scale notes: C - Db - Eb - F - Gb - Ab - Bb
Triads: Cdim - Db - Ebm - Fm - Gb - Ab - Bbm
7th chords: Cm7(b5) - Dbmaj7 - Ebm7 - Fm7 - Gbmaj7 - Ab7 - Bbm7
Tensions:
Cm7(b5) (b9*, 11, b13*)
Dbmaj7 (9, 11*, 13)
Ebm7 (9, 11, 13)
Fm7 (b9*, 11, b13*)
Gbmaj7 (9, #11, 13)
Ab7 (9, 11*, 13)
Bbm7 (9, 11, b13*)
(*denotes avoid notes)
IONIAN MODE (Natural minor scale's third degree)
The third Greek mode of the natural minor scale is the Ionian mode. To find its scale formula, we use the natural minor scale formula but start from the third degree (or simply the major scale formula). This gives the Ionian mode the following pattern:
whole tone - whole tone - semitone - whole tone - whole tone - whole tone - semitone.
For example, in the C Ionian mode, the sequence of notes would be C D E F G A B, and the formula can be represented numerically as:
1 2 3 4 5 6 7
This represents the root (1), major 2nd (2), major 3rd (3), perfect 4th (4), perfect 5th (5), major 6th (6), and major 7th (7). Each number corresponds to the interval between the root and the other six notes in the scale.
The Ionian mode’s defining chord is a major 7th chord (root, 3rd, 5th, 7th), and its characteristic note is the perfect 4th (extension 11), which distinguishes it from other major modes.
*The Ionian mode is the only Greek mode that has a major 7th chord in the first degree with a perfect 11th as an extension!
Now that we understand the formula for the Ionian mode, let’s explore the notes and chords generated by the C Ionian mode:
Scale notes: C - D - E - F - G - A - B
Triads: C - Dm - Em - F - G - Am - Bdim
7th chords: Cmaj7 - Dm7 - Em7 - Fmaj7 - G7 - Am7 - Bm7(b5)
Tensions:
Cmaj7 (9, 11*, 13)
Dm7 (9, 11, 13)
Em7 (b9*, 11, b13*)
Fmaj7 (9, #11, 13)
G7 (9, 11*, 13)
Am7 (9, 11, b13*)
Bm7(b5) (b9*, 11, b13*)
(*denotes avoid notes)
DORIAN MODE (Natural minor scale's fourth degree)
The fourth Greek mode of the natural minor scale is the Dorian mode. To find its scale formula, we use the minor scale formula but start from the fourth degree. This gives the Dorian mode the following pattern:
whole tone - semitone - whole tone - whole tone - whole tone - semitone - whole tone.
For example, in the C Dorian mode, the sequence of notes would be C D Eb F G A Bb, and the formula can be represented numerically as:
1 2 b3 4 5 6 b7
This represents the root (1), major 2nd (2), minor 3rd (b3), perfect 4th (4), perfect 5th (5), major 6th (6), and minor 7th (b7). Each number corresponds to the interval between the root and the other six notes in the scale.
The Dorian mode’s defining chord is a minor 7th chord (root, b3th, 5th, b7th), and its characteristic note is the major 6th (extension 13), which distinguishes it from other minor modes.
*The Dorian mode is the only Greek mode that has a minor 7th chord in the first degree with a major 13th as an extension!
Now that we understand the formula for the Dorian mode, let’s explore the notes and chords generated by the C Dorian mode:
Scale notes: C - D - Eb - F - G - A - Bb
Triads: Cm - Dm - Eb - F - Gm - Adim - Bb
7th chords: Cm7 - Dm7 - Ebmaj7 - F7 - Gm7 - Am7(b5) - Bbmaj7
Tensions:
Cm7 (9, 11, 13)
Dm7 (b9*, 11, b13*)
Ebmaj7 (9, #11, 13)
F7 (9, 11*, 13)
Gm7 (9, 11, b13*)
Am7(b5) (b9*, 11, b13*)
Bbmaj7 (9, 11*, 13)
(*denotes avoid notes)
PHRYGIAN MODE (Natural minor scale's fifth degree)
The fifth Greek mode of the natural minor scale is the Phrygian mode. To find its scale formula, we use the natural minor scale formula but start from the fifth degree. This gives the Phrygian mode the following pattern:
semitone - whole tone - whole tone - whole tone - semitone - whole tone - whole tone.
For example, in the C Phrygian mode, the sequence of notes would be C Db Eb F G Ab Bb, and the formula can be represented numerically as:
1 b2 b3 4 5 b6 b7
This represents the root (1), minor 2nd (b2), minor 3rd (b3), perfect 4th (4), perfect 5th (5), minor 6th (b6), and minor 7th (b7). Each number corresponds to the interval between the root and the other six notes in the scale.
The Phrygian mode’s defining chord is a minor 7th chord (root, b3th, 5th, b7th), and its characteristic note is the minor 2nd (extension b9), which distinguishes it from other minor modes.
*The Phrygian mode is the only Greek mode that has a minor 7th chord in the first degree with a minor 9th as an extension!
Now that we understand the formula for the Phrygian mode, let’s explore the notes and chords generated by the C Phrygian mode:
Scale notes: C - Db - Eb - F - G - Ab - Bb
Triads: Cm - Db - Eb - Fm - Gdim - Ab - Bbm
7th chords: Cm7 - Dbmaj7 - Eb7 - Fm7 - Gm7(b5) - Abmaj7 - Bbm7
Tensions:
Cm7 (b9*, 11, b13*)
Dbmaj7 (9, #11, 13)
Eb7 (9, 11*, 13)
Fm7 (9, 11, b13*)
Gm7(b5) (b9*, 11, b13*)
Abmaj7 (9, 11*, 13)
Bbm7 (9, 11, 13)
(*denotes avoid notes)
LYDIAN MODE (Natural minor scale's sixth degree)
The sixth Greek mode of the natural minor scale is the Lydian mode. To find its scale formula, we use the natural minor scale formula but start from the sixth degree. This gives the Lydian mode the following pattern:
whole tone - whole tone - whole tone - semitone - whole tone - whole tone - semitone.
For example, in the C Lydian mode, the sequence of notes would be C D E F# G A B, and the formula can be represented numerically as:
1 2 3 #4 5 6 7
This represents the root (1), major 2nd (2), major 3rd (3), augmented 4th (#4), perfect 5th (5), major 6th (6), and major 7th (7). Each number corresponds to the interval between the root and the other six notes in the scale.
The Lydian mode’s defining chord is a major 7th chord (root, 3rd, 5th, 7th), and its characteristic note is the augmented 4th (extension #11), which distinguishes it from other major modes.
*The Lydian mode is the only Greek mode that has a major 7th chord in the first degree with an augmented 11th as an extension!
Now that we understand the formula for the Lydian mode, let’s explore the notes and chords generated by the C Lydian mode:
Scale notes: C - D - E - F# - G - A - B
Triads: C - D - Em - F#dim - G - Am - Bm
7th chords: Cmaj7 - D7 - Em7 - F#m7(b5) - Gmaj7 - Am7 - Bm7
Tensions:
Cmaj7 (9, #11, 13)
D7 (9, 11*, 13)
Em7 (9, 11, b13*)
F#m7(b5) (b9*, 11, b13*)
Gmaj7 (9, 11*, 13)
Am7 (9, 11, 13)
Bm7 (b9*, 11, b13*)
(*denotes avoid notes)
MIXOLYDIAN MODE (Natural minor scale's seventh degree)
The seventh Greek mode of the natural minor scale is the Mixolydian mode. To find its scale formula, we use the natural minor scale formula but start from the seventh degree. This gives the Mixolydian mode the following pattern:
whole tone - whole tone - semitone - whole tone - whole tone - semitone - whole tone.
For example, in the C Mixolydian mode, the sequence of notes would be C D E F G A Bb, and the formula can be represented numerically as:
1 2 3 4 5 6 b7
This represents the root (1), major 2nd (2), major 3rd (3), perfect 4th (4), perfect 5th (5), major 6th (6), and minor 7th (b7). Each number corresponds to the interval between the root and the other six notes in the scale.
The Mixolydian mode’s defining chord is a dominant 7th chord (root, 3rd, 5th, b7th), and its characteristic note is the perfect 4th (extension 11), which distinguishes it from other major modes.
*The Mixolydian mode is the only Greek mode that has a dominant 7th chord in the first degree with a perfect 11th as an extension!
Now that we understand the formula for the Mixolydian mode, let’s explore the notes and chords generated by the C Mixolydian mode:
Scale notes: C - D - E - F - G - A - Bb
Triads: C - Dm - Edim - F - Gm - Am - Bb
7th chords: C7 - Dm7 - Em7(b5) - Fmaj7 - Gm7 - Am7 - Bbmaj7
Tensions:
C7 (9, 11*, 13)
Dm7 (9, 11, b13*)
Em7(b5) (b9*, 11, b13*)
Fmaj7 (9, 11*, 13)
Gm7 (9, 11, 13)
Am7 (b9*, 11, b13*)
Bbmaj7 (9, #11, 13)
(*denotes avoid notes)
CHART OF GREEK MODES (NATURAL MINOR SCALE) |
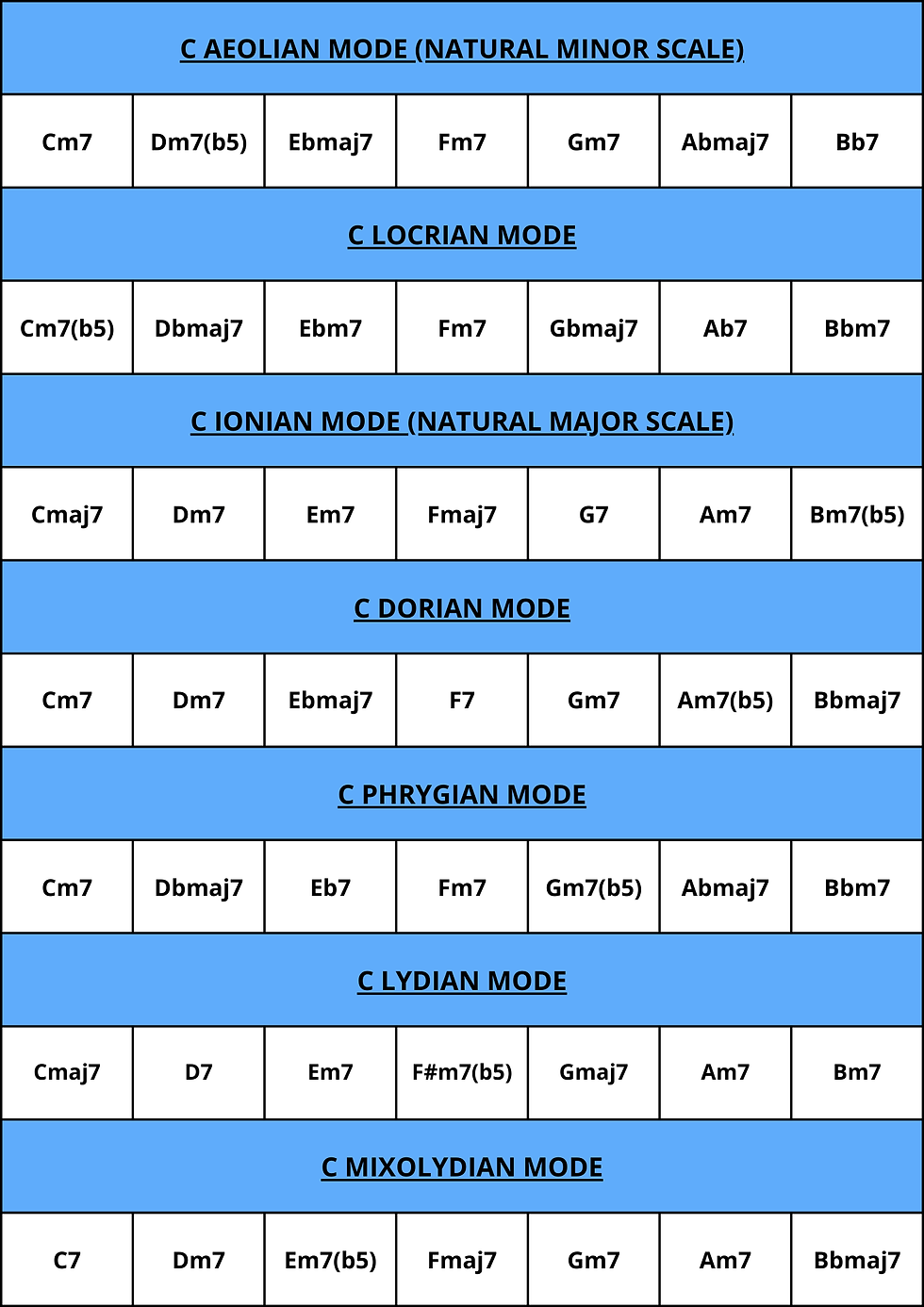
GREEK MODES FROM THE HARMONIC MINOR SCALE
As we covered in the article on "Harmonic Minor Keys", the harmonic minor scale differs from the natural minor scale by just one note. However, this small change significantly alters the character of many chords and introduces new variations of the original modes.
HARMONIC MINOR SCALE (Harmonic minor scale's first degree)
The first mode of the harmonic minor scale is simply known by the name of the scale itself. To determine its scale formula, we use the formula for the harmonic minor scale, starting from the first degree. The pattern is as follows:
whole tone - semitone - whole tone - whole tone - semitone - *(wt + st) - semitone.
*(wt + st) = 1 whole tone + 1 semitone
For example, in the C Harmonic minor scale, the sequence of notes would be C D Eb F G Ab B, and the formula can be represented numerically as:
1 2 b3 4 5 b6 7
This represents the root (1), major 2nd (2), minor 3rd (b3), perfect 4th (4), perfect 5th (5), minor 6th (b6), and major 7th (7). Each number corresponds to the interval between the root and the other six notes in the scale.
The Harmonic minor scale’s defining chord is a minor (major 7th) chord (root, b3rd, 5th, 7th), and its characteristic note is the minor 6th (extension b13), which distinguishes it from other minor modes.
*The Harmonic minor scale is the only scale/mode that has a minor (major 7th) chord in the first degree with a minor 13th as an extension!
Now that we understand the formula for the Harmonic minor scale, let’s explore the notes and chords generated by the C Harmonic minor scale:
Scale notes: C - D - Eb - F - G - Ab - B
Triads: Cm - Ddim - Eb(#5) - Fm - G - Ab - Bdim
7th chords: Cm(maj7) - Dm7(b5) - Ebmaj7(#5) - Fm7 - G7 - Abmaj7 - Bdim7
Tensions:
Cm(maj7) (9, 11, b13*)
Dm7(b5) (b9*, 11, 13)
Ebmaj7(#5) (9, 11*, 13*)
Fm7 (9, #11, 13)
G7 (b9, 11*, b13)
Abmaj7 (#9, #11, 13)
Bdim7 (b9*, b11*, b13)
(*denotes avoid notes)
LOCRIAN 6 MODE (Harmonic minor scale's second degree)
The second mode of the harmonic minor scale is the Locrian 6 mode. To find its scale formula, we use the harmonic minor scale formula but start from the second degree. This gives the Locrian 6 mode the following pattern:
semitone - whole tone - whole tone - semitone - *(wt + st) - semitone - whole tone.
*(wt + st) = 1 whole tone + 1 semitone
For example, in the C Locrian 6 scale, the sequence of notes would be C Db Eb F Gb A Bb, and the formula can be represented numerically as:
1 b2 b3 4 b5 6 b7
This represents the root (1), minor 2nd (b2), minor 3rd (b3), perfect 4th (4), diminished 5th (b5), major 6th (6), and minor 7th (b7). Each number corresponds to the interval between the root and the other six notes in the scale.
The Locrian 6 mode’s defining chord is a minor 7th (b5) chord (root, b3rd, b5th, b7th), and its characteristic note is the major 6th (extension 13), which distinguishes it from other minor modes.
*The Locrian 6 mode is the only Greek mode that has a minor 7th (b5) chord in the first degree with a major 13th as an extension!
Now that we understand the formula for the Locrian 6 mode, let’s explore the notes and chords generated by the C Locrian 6 mode:
Scale notes: C - Db - Eb - F - Gb - A - Bb
Triads: Cdim - Db(#5) - Ebm - F - Gb - Adim - Bbm
7th chords: Cm7(b5) - Dbmaj7(#5) - Ebm7 - F7 - Gbmaj7 - Adim7 - Bbm(maj7)
Tensions:
Cm7(b5) (b9*, 11, 13)
Dbmaj7(#5) (9, 11*, 13*)
Ebm7 (9, #11, 13)
F7 (b9, 11*, b13)
Gbmaj7 (#9, #11, 13)
Adim7 (b9*, b11*, b13)
Bbm(maj7) (9, 11, b13*)
(*denotes avoid notes)
IONIAN AUGMENTED MODE (Harmonic minor scale's third degree)
The third mode of the harmonic minor scale is the Ionian augmented mode. To find its scale formula, we use the harmonic minor scale formula but start from the third degree. This gives the Ionian augmented mode the following pattern:
whole tone - whole tone - semitone - *(wt + st) - semitone - whole tone - semitone.
*(wt + st) = 1 whole tone + 1 semitone
For example, in the C Ionian augmented mode, the sequence of notes would be C D E F G# A B, and the formula can be represented numerically as:
1 2 3 4 #5 6 7
This represents the root (1), major 2nd (2), major 3rd (3), perfect 4th (4), augmented 5th (#5), major 6th (6), and major 7th (7). Each number corresponds to the interval between the root and the other six notes in the scale.
The Ionian augmented mode’s defining chord is a major 7th (#5) chord (root, b3rd, #5th, 7th), and its characteristic note is the perfect 4th (extension 11), which distinguishes it from other major modes.
*The Ionian augmented mode is the only Greek mode that has a major 7th (#5) chord in the first degree with a perfect 11th as an extension!
Now that we understand the formula for the Ionian augmented mode, let’s explore the notes and chords generated by the C Ionian augmented mode:
Scale notes: C - D - E - F - G# - A - B
Triads: C(#5) - Dm - E - F - G#dim - Am - Bdim
7th chords: Cmaj7(#5) - Dm7 - E7 - Fmaj7 - G#dim7 - Am(maj7) - Bm7(b5)
Tensions:
Cmaj7(#5) (9, 11*, 13*)
Dm7 (9, #11, 13)
E7 (b9, 11*, b13)
Fmaj7 (#9, #11, 13)
G#dim7 (b9*, b11*, b13)
Am(maj7) (9, 11, b13*)
Bm7(b5) (b9*, 11, 13)
(*denotes avoid notes)
DORIAN #4 MODE (Harmonic minor scale's fourth degree)
The fourth mode of the harmonic minor scale is the Dorian #4 mode. To find its scale formula, we use the harmonic minor scale formula but start from the fourth degree. This gives the Dorian #4 mode the following pattern:
whole tone - semitone - *(wt + st) - semitone - whole tone - semitone - whole tone.
*(wt + st) = 1 whole tone + 1 semitone
For example, in the C Dorian #4 mode, the sequence of notes would be C D Eb F# G A Bb, and the formula can be represented numerically as:
1 2 b3 #4 5 6 b7
This represents the root (1), major 2nd (2), minor 3rd (b3), augmented 4th (#4), perfect 5th (5), major 6th (6), and minor 7th (b7). Each number corresponds to the interval between the root and the other six notes in the scale.
The Dorian #4 mode’s defining chord is a minor 7th chord (root, b3rd, 5th, b7th), and its characteristic note is the augmented 4th (extension #11), which distinguishes it from other minor modes.
*The Dorian #4 mode is the only Greek mode that has a minor 7th chord in the first degree with an augmented 11th as an extension!
Now that we understand the formula for the Dorian #4 mode, let’s explore the notes and chords generated by the C Dorian #4 mode:
Scale notes: C - D - Eb - F# - G - A - Bb
Triads: Cm - D - Eb - F#dim - Gm - Adim - Bb(#5)
7th chords: Cm7 - D7 - Ebmaj7 - F#dim7 - Gm(maj7) - Am7(b5) - Bbmaj7(#5)
Tensions:
Cm7 (9, #11, 13)
D7 (b9, 11*, b13)
Ebmaj7 (#9, #11, 13)
F#dim7 (b9*, b11*, b13)
Gm(maj7) (9, 11, b13*)
Am7(b5) (b9*, 11, 13)
Bbmaj7(#5) (9, 11*, 13*)
(*denotes avoid notes)
MIXOLYDIAN b2b6 MODE (Harmonic minor scale's fifth degree)
The fifth mode of the harmonic minor scale is the Mixolydian b2 b6 mode. To find its scale formula, we use the harmonic minor scale formula but start from the fifth degree. This gives the Mixolydian b2 b6 mode the following pattern:
semitone - *(wt + st) - semitone - whole tone - semitone - whole tone - whole tone.
*(wt + st) = 1 whole tone + 1 semitone
For example, in the C Mixolydian b2 b6 mode, the sequence of notes would be C Db E F G Ab Bb, and the formula can be represented numerically as:
1 b2 3 4 5 b6 b7
This represents the root (1), minor 2nd (b2), major 3rd (3), perfect 4th (4), perfect 5th (5), minor 6th (b6), and minor 7th (b7). Each number corresponds to the interval between the root and the other six notes in the scale.
The Mixolydian b2 b6 mode’s defining chord is a dominant 7th chord (root, 3rd, 5th, b7th), and its characteristic notes are the minor 2nd (extension b9) and the minor 6th (extensions b13), which distinguishes it from other major modes.
*The Mixolydian b2 b6 mode is the only Greek mode that has a dominant 7th chord in the first degree with a minor 9th and a minor 13th as extensions!
Now that we understand the formula for the Mixolydian b2 b6 mode, let’s explore the notes and chords generated by the C Mixolydian b2 b6 mode:
Scale notes: C - Db - E - F - G - Ab - Bb
Triads: C - Db - Edim - Fm - Gdim - Ab(#5) - Bbm
7th chords: C7 - Dbmaj7 - Edim7 - Fm(maj7) - Gm7(b5) - Abmaj7(#5) - Bbm7
Tensions:
C7 (b9, 11*, b13)
Dbmaj7 (#9, #11, 13)
Edim7 (b9*, b11*, b13)
Fm(maj7) (9, 11, b13*)
Gm7(b5) (b9*, 11, 13)
Abmaj7(#5) (9, 11*, 13*)
Bbm7 (9, #11, 13)
(*denotes avoid notes)
LYDIAN #2 MODE (Harmonic minor scale's sixth degree)
The sixth mode of the harmonic minor scale is the Lydian #2 mode. To find its scale formula, we use the harmonic minor scale formula but start from the sixth degree. This gives the Lydian #2 mode the following pattern:
*(wt + st) - semitone - whole tone - semitone - whole tone - whole tone - semitone.
*(wt + st) = 1 whole tone + 1 semitone
For example, in the C Lydian #2 mode, the sequence of notes would be C D# E F# G A B, and the formula can be represented numerically as:
This represents the root (1), augmented 2nd (#2), major 3rd (3), augmented 4th (#4), perfect 5th (5), major 6th (6), and major 7th (7). Each number corresponds to the interval between the root and the other six notes in the scale.
The Lydian #2 mode’s defining chord is a major 7th chord (root, 3rd, 5th, 7th), and its characteristic notes are the augmented 2nd (extension #9) and the augmented 4th (extensions #11), which distinguishes it from other major modes.
*The Lydian #2 mode is the only Greek mode that has a major 7th chord in the first degree with an augmented 9th and an augmented 11th as extensions!
Now that we understand the formula for the Lydian #2 mode’, let’s explore the notes and chords generated by the C Lydian #2 mode:
Scale notes: C - D# - E - F# - G - A - B
Triads: C - D#dim - Em - F#dim - G(#5) - Am - B
7th chords: Cmaj7 - D#dim7- Em(maj7) - F#m7(b5) - Gmaj7(#5) - Am7 - B7
Tensions:
Cmaj7 (#9, #11, 13)
D#dim7 (b9*, b11*, b13)
Em(maj7) (9, 11, b13*)
F#m7(b5) (b9*, 11, 13)
Gmaj7(#5) (9, 11*, 13*)
Am7 (9, #11, 13)
B7 (b9, 11*, b13)
(*denotes avoid notes)
SUPER LOCRIAN bb7 AKA HARMONIC DIMINSHED SCALE (Harmonic minor scale's seventh degree)
The seventh mode of the harmonic minor scale is the Super Locrian bb7 mode. To find its scale formula, we use the harmonic minor scale formula but start from the seventh degree. This gives the Harmonic minor diminished mode the following pattern:
semitone - whole tone - semitone - whole tone - whole tone - semitone - *(wt + st).
*(wt + st) = 1 whole tone + 1 semitone
For example, in the C Super Locrian bb7 mode, the sequence of notes would be C Db Eb Fb Gb Ab Bbb, and the formula can be represented numerically as:
1 b2 b3 b4 b5 b6 bb7
This represents the root (1), minor 2nd (b2), minor 3rd (b3), diminished 4th (b4), diminished 5th (b5), minor 6th (b6), and diminished 7th (bb7). Each number corresponds to the interval between the root and the other six notes in the scale.
The Super Locrian bb7 mode’s defining chord is a diminished 7th chord (root, b3rd, b5th, bb7th), and its characteristic notes are the diminished 2nd (extension b9) and the diminished 4th (extensions b11), which distinguishes it from other major modes.
*The Super Locrian bb7 mode is the only Greek mode that has a diminished 7th chord in the first degree with a minor 9th and a diminished 11th as extensions!
Now that we understand the formula for the Super Locrian bb7 mode, let’s explore the notes and chords generated by the C Super Locrian bb7 mode:
Scale notes: C - Db - Eb - Fb - Gb - Ab - Bbb
Triads: Cdim - Dbm - Ebdim - Fb(#5) - Gbm - Ab - Bbb
7th chords: Cdim7 - Dbm(maj7)- Ebm7(b5) - Fb(#5)- Gbm7 - Ab7 - Bbbmaj7
Tensions:
Cdim7 (b9*, b11*, b13)
Dbm(maj7) (9, 11, b13*)
Ebm7(b5) (b9*, 11, 13)
Fbmaj7(#5) (9, 11*, 13*)
Gb7 (9, #11, 13)
Ab7 (b9, 11*, b13)
Bbbmaj7 (#9, #11, 13)
(*denotes avoid notes)
CHART OF GREEK MODES (HARMONIC MINOR SCALE) |
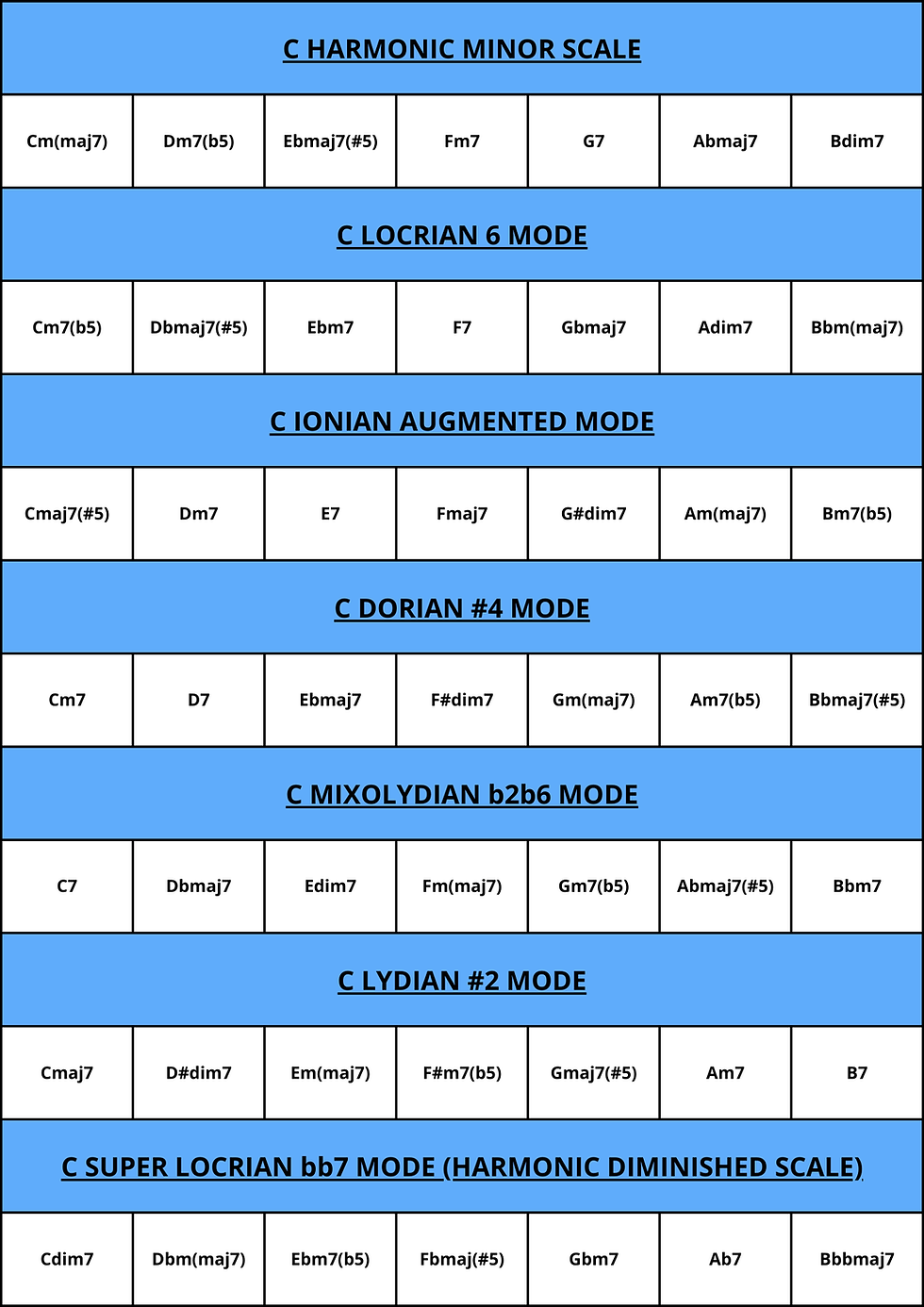
GREEK MODES FROM THE MELODIC MINOR SCALE
As discussed in our article on "Melodic Minor Keys," the melodic minor scale differs from the natural minor scale by just two notes, and it closely resembles the major scale, with the only difference being the third degree. However, this small alteration significantly changes the character of many chords and, as with the harmonic minor scale, introduces new variations of the original modes.
MELODIC MINOR SCALE (Melodic minor scale's first degree)
Just like the harmonic minor scale, the first mode of the melodic minor scale is simply known by the name of the scale itself. To determine its scale formula, we use the formula for the melodic minor scale, starting from the first degree. The pattern is as follows:
whole tone - semitone - whole tone - whole tone - whole tone - whole tone - semitone.
For example, in the C Melodic minor scale, the sequence of notes would be C D Eb F G A B, and the formula can be represented numerically as:
1 2 b3 4 5 6 7
This represents the root (1), major 2nd (2), minor 3rd (b3), perfect 4th (4), perfect 5th (5), major 6th (6), and major 7th (7). Each number corresponds to the interval between the root and the other six notes in the scale.
The Melodic minor scale’s defining chord is a minor (major 7th) chord (root, b3rd, 5th, 7th), and its characteristic note is the major 6th (extension 13), which distinguishes it from other minor modes.
*The Melodic minor scale is the only scale/mode that has a minor (major 7th) chord in the first degree with a major 13th as an extension!
Now that we understand the formula for the Melodic minor scale, let’s explore the notes and chords generated by the C Melodic minor scale:
Scale notes: C - D - Eb - F - G - A - B
Triads: Cm - Dm - Eb(#5) - F - G - Adim - Bdim
7th chords: Cm(maj7) - Dm7 - Ebmaj7(#5) - F7 - G7 - Am7(b5) - Bm7(b5)
Tensions:
Cm(maj7) (9, 11, 13)
Dm7 (b9*, 11, 13)
Ebmaj7(#5) (9, #11, 13*)
F7 (9, #11, 13)
G7 (b9, 11*, 13)
Am7(b5) (9, 11, b13)
Bm7(b5) (b9*, b11*, b13)
(*denotes avoid notes)
DORIAN b2 AKA PHRYGIAN 6 MODE (Melodic minor scale's second degree)
The second mode of the melodic minor scale is the Dorian b2 mode. To find its scale formula, we use the melodic minor scale formula but start from the second degree. This gives the Dorian b2 mode the following pattern:
semitone - whole tone - whole tone - whole tone - whole tone - semitone - whole tone.
For example, in the C Dorian b2 mode, the sequence of notes would be C Db Eb F G A Bb, and the formula can be represented numerically as:
1 b2 b3 4 5 6 b7
This represents the root (1), minor 2nd (b2), minor 3rd (b3), perfect 4th (4), perfect 5th (5), major 6th (6), and minor 7th (b7). Each number corresponds to the interval between the root and the other six notes in the scale.
The Dorian b2 mode’s defining chord is a minor 7th chord (root, b3rd, 5th, b7th), and its characteristic notes are the minor 2nd (extension b9) and the major 6th (extensions 13), which distinguishes it from other minor modes.
*The Dorian b2 mode is the only Greek mode that has a minor 7th chord in the first degree with a minor 9th and a major 13th as extensions!
Now that we understand the formula for the Dorian b2 mode, let’s explore the notes and chords generated by the C Dorian b2 mode:
Scale notes: C - Db - Eb - F - G - A - Bb
Triads: Cm - Db(#5) - Eb - F - Gdim - Adim - Bbm
7th chords: Cm7 - Dbmaj7(#5) - Eb7 - F7 - Gm7(b5) - Am7(b5) - Bbm(maj7)
Tensions:
Cm7 (b9*, 11, 13)
Dbmaj7(#5) (9, #11, 13*)
Eb7 (9, #11, 13)
F7 (b9, 11*, 13)
Gm7(b5) add 9, add 11, add b13)
Am7(b5) (b9*, b11*, b13)
Bbm(maj7) (9, 11, 13)
(*denotes avoid notes)
LYDIAN AUGMENTED MODE (Melodic minor scale's third degree)
The third mode of the melodic minor scale is the Lydian augmented mode. To find its scale formula, we use the melodic minor scale formula but start from the third degree. This gives the Lydian augmented mode the following pattern:
whole tone - whole tone - whole tone - whole tone - semitone - whole tone - semitone.
For example, in the C Lydian augmented mode, the sequence of notes would be C D E F# G# A B, and the formula can be represented numerically as:
This represents the root (1), major 2nd (2), major 3rd (3), augmented 4th (#4), augmented 5th (#5), major 6th (6), and major 7th (7). Each number corresponds to the interval between the root and the other six notes in the scale.
The Lydian augmented mode’s defining chord is a major 7th (#5) chord (root, 3rd, #5th, 7th), and its characteristic note is the augmented #4 (extension #11), which distinguishes it from other major modes.
*The Lydian augmented mode is the only Greek mode that has a major 7th (#5) chord in the first degree with an augmented 11th as an extension!
Now that we understand the formula for the Lydian augmented mode, let’s explore the notes and chords generated by the C Lydian augmented mode:
Scale notes: C - D - E - F# - G# - A - B
Triads: C(#5) - D - E - F#dim - G#dim - Am - Bm
7th chords: Cmaj7(#5) - D7 - E7 - F#m7(b5) - G#m7(b5) - Am(maj7) - Bm7
Tensions:
Cmaj7(#5) (9, #11, 13*)
D7 (9, #11, 13)
E7 (b9, 11*, 13)
F#m7(b5) (9, 11, b13)
G#m7(b5) (b9*, b11*, b13)
Am(maj7) (9, 11, 13)
Bm7 (b9*, 11, 13)
(*denotes avoid notes)
MIXOLYDIAN #4 MODE (Melodic minor scale's fourth degree)
The fourth mode of the melodic minor scale is the Mixolydian #4 mode. To find its scale formula, we use the melodic minor scale formula but start from the fourth degree. This gives the Mixolydian #4 mode the following pattern:
whole tone - whole tone - whole tone - semitone - whole tone - semitone - whole tone.
For example, in the C Mixolydian #4 mode, the sequence of notes would be C D E F# G A Bb, and the formula can be represented numerically as:
1 2 3 #4 5 6 b7
This represents the root (1), major 2nd (2), major 3rd (3), augmented 4th (#4), perfect 5th (5), major 6th (6), and minor 7th (b7). Each number corresponds to the interval between the root and the other six notes in the scale.
The Mixolydian #4 mode’s defining chord is a dominant 7th chord (root, 3rd, 5th, b7th), and its characteristic note is the augmented #4 (extension #11), which distinguishes it from other major modes.
*The Mixolydian #4 mode is the only Greek mode that has a dominant 7th chord in the first degree with an augmented 11th as an extension!
Now that we understand the formula for the Mixolydian #4 mode, let’s explore the notes and chords generated by the C Mixolydian #4 mode:
Scale notes: C - D - E - F# - G - A - Bb
Triads: C - D - Edim - F#dim - Gm - Am - Bb(#5)
7th chords: C7 - D7 - Em7(b5) - F#m7(b5) - Gm(maj7) - Am7 - Bbmaj7(#5)
Tensions:
C7 (9, #11, 13)
D7 (b9, 11*, 13)
Em7(b5) (9, 11, b13)
F#m7(b5) (b9*, b11*, b13)
Gm(maj7) (9, 11, 13)
Am7 (b9*, 11, 13)
Bbmaj7(#5) (9, #11, 13*)
(*denotes avoid notes)
MIXOLYDIAN b6 MODE (Melodic minor scale's fifth degree)
The fifth mode of the melodic minor scale is the Mixolydian b6 mode. To find its scale formula, we use the melodic minor scale formula but start from the fifth degree. This gives the Mixolydian b6 mode the following pattern:
whole tone - whole tone - semitone - whole tone - semitone - whole tone - whole tone.
For example, in the C Mixolydian b6 mode, the sequence of notes would be C D E F G Ab Bb, and the formula can be represented numerically as:
1 2 3 4 5 b6 b7
This represents the root (1), major 2nd (2), major 3rd (3), perfect 4th (4), perfect 5th (5), minor 6th (b6), and minor 7th (b7). Each number corresponds to the interval between the root and the other six notes in the scale.
The Mixolydian b6 mode’s defining chord is a dominant 7th chord (root, 3rd, 5th, b7th), and its characteristic notes are the minor 2nd (extension b9) and the minor 6th (extension b13), which distinguishes it from other major modes.
*The Mixolydian b6 mode is the only Greek mode that has a dominant 7th chord in the first degree with a major 9th and a minor 13th as extensions!
Now that we understand the formula for the Mixolydian b6 mode, let’s explore the notes and chords generated by the C Mixolydian b6 mode:
Scale notes: C - D - E - F - G - Ab - Bb
Triads: C - Ddim - Edim - Fm - Gm - Ab(#5) - Bb
7th chords: C7 - Dm7(b5) - Em7(b5) - Fm(maj7) - Gm7 - Abmaj7(#5) - Bb7
Tensions:
C7 (b9, 11*, 13)
Dm7(b5) (9, 11, b13)
Em7(b5) (b9*, b11*, b13)
Fm(maj7) (9, 11, 13)
Gm7 (b9*, 11, 13)
Abmaj7(#5) (9, #11, 13*)
Bb7 (9, #11, 13)
(*denotes avoid notes)
LOCRIAN 2 MODE (Melodic minor scale's sixth degree)
The sixth mode of the melodic minor scale is the Locrian 2 mode. To find its scale formula, we use the melodic minor scale formula but start from the sixth degree. This gives the Locrian 2 mode the following pattern:
whole tone - semitone - whole tone - semitone - whole tone - whole tone - whole tone.
For example, in the C Locrian 2 mode, the sequence of notes would be C D Eb F Gb Ab Bb, and the formula can be represented numerically as:
1 2 b3 4 b5 b6 b7
This represents the root (1), major 2nd (2), minor 3rd (b3), perfect 4th (4), diminished 5th (b5), minor 6th (b6), and minor 7th (b7). Each number corresponds to the interval between the root and the other six notes in the scale.
The Locrian 2 mode’s defining chord is a minor 7th (b5) chord (root, b3rd, b5th, b7th), and its characteristic notes are the major 2nd (extension 9) and the minor 6th (extension b13), which distinguishes it from other minor modes.
*The Locrian 6 mode is the only Greek mode that has a minor 7th (b5) chord in the first degree with a minor 9th and a minor 13th as extensions!
Now that we understand the formula for the Locrian 2 mode, let’s explore the notes and chords generated by the C Locrian 2 mode:
Scale notes: C - D - Eb - F - Gb - Ab - Bb
Triads: Cdim - Ddim - Ebm - Fm - Gb(#5) - Ab - Bb
7th chords: Cm7(b5) - Dm7(b5) - Ebm(maj7) - Fm7 - Gbmaj7(#5) - Ab7 - Bb7
Tensions:
Cm7(b5) (9, 11, b13)
Dm7(b5) (b9*, b11*, b13)
Ebm(maj7) (9, 11, 13)
Fm7 (b9*, 11, 13)
Gbmaj7(#5) (9, #11, 13*)
Ab7 (9, #11, 13)
Bb7 (b9, 11*, 13)
(*denotes avoid notes)
SUPER LOCRIAN MODE AKA ALTERED SCALE (Melodic minor scale's seventh degree)
The seventh mode of the melodic minor scale is the Super Locrian mode (I'll explain about the altered scale when we get to the "other types of chords" section). To find its scale formula, we use the melodic minor scale formula but start from the seventh degree. This gives the Super Locrian mode the following pattern:
semitone - whole tone - semitone - whole tone - whole tone - whole tone - whole tone.
For example, in the C Super Locrian mode, the sequence of notes would be C Db Eb Fb Gb Ab Bb, and the formula can be represented numerically as:
1 b2 b3 b4 b5 b6 b7
This represents the root (1), minor 2nd (b2), minor 3rd (b3), diminished 4th (b4), diminished 5th (b5), minor 6th (b6), and minor 7th (b7). Each number corresponds to the interval between the root and the other six notes in the scale.
The Super Locrian mode’s defining chord is a minor 7th (b5) chord (root, b3rd, b5th, b7th), and its characteristic notes are the diminished 4th (extension b11) and the minor 6th (extension b13), which distinguishes it from other minor modes.
*The Super Locrian mode is the only Greek mode that has a minor 7th (b5) chord in the first degree with a diminished 11th and a minor 13th as extensions!
Now that we understand the formula for the Super Locrian mode, let’s explore the notes and chords generated by the C Super Locrian mode:
Scale notes: C - Db - Eb - Fb - Gb - Ab - Bb
Triads: Cdim - Dbm - Ebm - Fb(#5) - Gb - Ab - Bbdim
7th chords: Cm7(b5) - Dbm(maj7) - Ebm7 - Fbmaj7(#5) - Gb7 - Ab7 - Bbm7(b5)
Tensions:
Cm7(b5) (b9*, b11*, b13)
Dbm(maj7) (9, 11, 13)
Ebm7 (b9*, 11, 13)
Fbmaj7(#5) (9, #11, 13*)
Gb7 (9, #11, 13)
Ab7 (b9, 11*, 13)
Bbm7(b5) (9, 11, b13)
(*denotes avoid notes)
CHART OF GREEK MODES (MELODIC MINOR SCALE) |
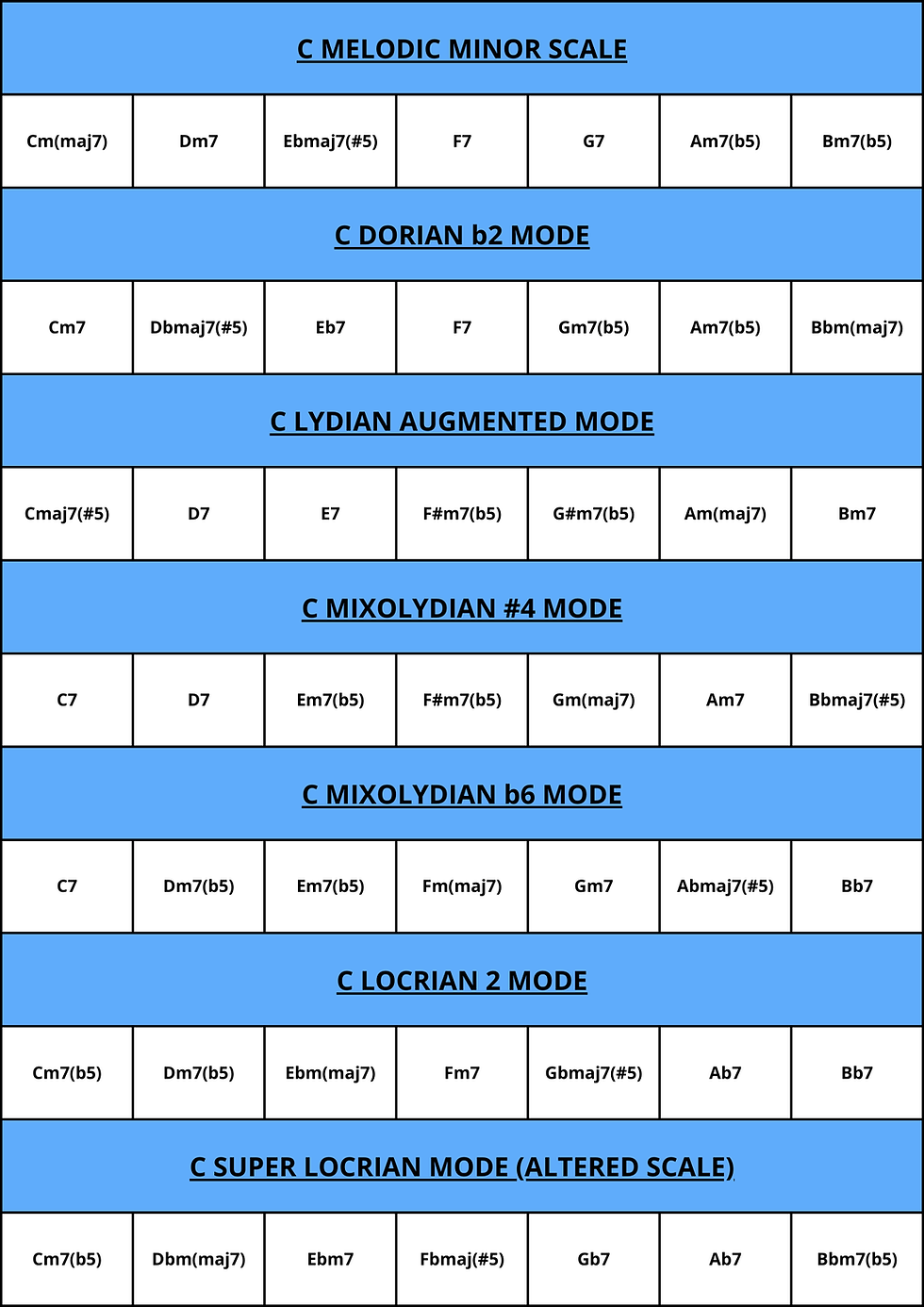
OTHER TYPES OF CHORDS
Although we've covered the origins of all chords and modes in this and the previous three articles, you may have noticed that certain chords—like Sus4, Sus2, 7sus4, Lydian triads, Phrygian triads, major and minor 6ths, and altered chords—weren't explicitly mentioned. In fact, they were; it's simply a different perspective on the chords we've already explored. In this section, I'll explain each of them in detail.
SUSPENDED CHORDS
Triads are typically formed by combining the root, 3rd, and 5th degrees, while 7th chords add an additional note, the 7th degree, to this basic structure.
Example of a triad: The C major triad, or simply "C", consists of its root (C), major 3rd (E), and perfect 5th (G).
Example of a 7th chord: The C dominant 7th, or "C7", includes its root (C), major 3rd (E), perfect 5th (G), and minor 7th (Bb).
A suspended chord replaces the 3rd degree with either the 4th or 2nd degree, “suspending” the typical 3rd.
Here are all the triads and 7th chords in the key of C major that we’ve worked with so far:
Triads: C, Dm, Em, F, G, Am, Bdim
7th chords: Cmaj7, Dm7, Em7, Fmaj7, G7, Am7, Bm7(b5)
Each of these chords has a "suspended" version, regardless of its quality (major, minor, diminished, etc.):
Suspended triads: Csus4, Dsus4, Esus4, Fsus#4, Gsus4, Asus4, Bsus4(b5)
Suspended 7th chords: Cmaj7sus4, D7sus4, E7sus4, Fmaj7sus#4, G7sus4, A7sus4, B7sus4(b5)
When we replace the 3rd with the 2nd, we get:
Triads with sus2: Csus2, Dsus2, Esusb2, Fsus2, Gsus2, Asus2, Bsus2(b5)
7th chords with sus2: Cmaj7sus2, D7sus2, E7susb2, Fmaj7sus2, G7sus2, A7sus2, B7sus2(b5)
Notes:
All of these chords can be combined with the original triads and 7th chords when writing music or accompanying a soloist or singer.
When we replace the 3rd with the 4th or 2nd, the original 3rd becomes a tension (the 10th for a major 3rd, or b10th for a minor 3rd), while the 4th or 2nd becomes a chord tone.
If you've followed this series from the start, you'll notice that the Esusb2 triad is what we call a "Phrygian triad." This is because it originates from the third degree of the major scale, which is also the origin of the Phrygian mode. Some people might notate this chord as E(b2).
The Fsus#4 is called a Lydian triad because it originates from the fourth degree of the major scale and contains the mode's characteristic #4 note. Some people write this as F(b5), since #4 and b5 are enharmonic equivalents.
You might notice that when transforming major 7th chords into suspended chords, I kept the "maj" designation (e.g., Cmaj7 becomes Cmaj7sus4). However, for minor chords, I omitted the "m" (e.g., Dm7 becomes D7sus4). This is because when you see D7sus4, it's understood that the 7th is minor, just like in a dominant 7th chord (e.g., G7). For sus chords with a major 7th, we explicitly state "maj" to highlight the difference.
SIXTH CHORDS
The process of understanding sixth chords is quite similar to that of suspended chords. Sixth chords are essentially 7th chords where the 7th degree is replaced by the 6th degree. As a result, each chord can have its own "sixth" version. Using the chords from the key of C major as an example:
7th chords: Cmaj7, Dm7, Em7, Fmaj7, G7, Am7, Bm7(b5)
By replacing the 7th with the 6th in each chord, we get:
Sixth chords: C6, Dm6, Em(b6), F6, G6, Am(b6), Bm(b5)b6
Notes:
Similar to suspended chords, sixth chords can be combined with their original forms to create a variety of chord progressions.
While it's less common to use minor sixth chords (e.g., Em(b6), Am(b6), and Bm(b6)b5), major chords with the major sixth (e.g., C6, F6, G6) and minor chords with the major sixth (e.g., Dm6) are much more frequently used. There’s a reason for this, which I’ll explain in more detail when we discuss important chord progressions in the next article.
#4 VS. b5
As I mentioned earlier, the #4 and b5 are enharmonic equivalents, meaning they share the same pitch but have different names. This allows any chord with a #11 (the extension of the 4th degree) to be interpreted in different ways.
For example, the fourth degree of the C major scale, Fmaj7, has a #11 available, so it can also be viewed as Fmaj7(b5). Another example is the third degree of the C melodic minor scale, Ebmaj7(#5), which also has a #11 available, allowing it to be interpreted as Ebmaj7(b5). Similarly, the fourth degree of the C melodic minor scale, F7, can be interpreted as F7(b5), and so on. As a general rule, the #4 can be interpreted as a b5.
You might be wondering: "But what's the point? Aren't they the same chord?" Well, not exactly. The sound of an Fmaj7(b5) chord differs from that of an Fmaj7 chord because we're replacing a chord tone. The Fmaj7(b5) is essentially the same as "Fmaj7(#11) omitted 5th", but it’s more convenient to notate it as Fmaj7(b5). Additionally, for an improviser, the correct chord name is crucial. Interpreting the #4 as a b5 means that this note is now considered a chord tone, while the perfect 5th becomes a tension (the 12th) and should treated as an avoid note since it is a semitone above a chord tone. Therefore, when using the Lydian mode to improvise over a maj7(b5) chord, the perfect 5th should be used only as a passing note.
ALTERED CHORDS
Altered chords are characterized by having either a b5 or #5 as chord tones, along with b9 and #9 as tensions. Earlier, I mentioned that I’d explain more about the seventh degree of the melodic minor scale—now is the perfect time to dive into that.
Initially, we interpret this mode as consisting of a root (1), minor 2nd (b2), minor 3rd (b3), diminished 4th (b4), diminished 5th (b5), minor 6th (b6), and minor 7th (b7):
1 b2 b3 b4 b5 b6 b7
Many people refer to this as the Super Locrian mode, as it forms a m7(b5) chord, differing from other Locrian modes due to its diminished 4th. However, this interpretation is rarely used in practice. Instead, we typically interpret the diminished 4th as a major 3rd (since they are enharmonic equivalents, just like the #4 and b5). Also, because a chord can’t have both a minor and major 3rd, we reinterpret the b3 as a #2. This gives us the following sequence:
*Note: There is no 6th in this sequence.
This mode forms a dominant 7th (#5) chord (e.g., C7(#5)), with tensions of b9, #9, and #11—and no avoid notes!
Now, remember when I mentioned that any chord with a #11 can use it as a b5? This applies here too. Consequently, the #5 must be interpreted as a b6, since a chord can’t contain two different 5ths. With this, we can also rewrite the mode as:
1 b2 #2 3 b5 b6 b7
*Note: There are no fourths in this sequence now.
This version of the mode forms a dominant 7th (b5) chord (e.g., C7(b5)), with tensions of b9, #9, and b13—and again, no avoid notes!
Key Points:
The altered scale (or mode) is the most appropriate choice when playing over dominant 7th (#5) or dominant 7th (b5) chords.
When you see the notation "Alt." (e.g., C7alt.), the composer is giving you the flexibility to interpret the chord as either C7(#5) or C7(b5), but the scale to use is always the altered scale.
HOW TO PRACTICE/USE THE GREEK MODES?
Many instructors and music books often recommend starting by mapping the major scale across the fretboard using modes. However, I’m not a fan of this approach because students tend to memorize the modes as seven disconnected patterns, which makes it difficult for them to link these shapes together when soloing. Even if they become comfortable playing in one key, transposing the seven modes to another key can feel overwhelming, causing many to give up. I highly recommend checking out my article on "Guitar Scales," where I explain how to play each mode, the key positions, and how to internalize their sounds. Pay particular attention to the "Life Hack" section, where I show you a trick to reduce the seven shapes to five, using the root note as a reference.
Modes are primarily used for composing modal songs and improvisation. Composing in a modal style is quite simple: you stick to the chords and notes of the mode you want to use. For example, if I want to compose a song in C major with a Lydian sound (refer back to the C Lydian chords):
Scale notes: C - D - E - F# - G - A - B
Triads: C - D - Em - F#dim - G - Am - Bm
7th chords: Cmaj7 - D7 - Em7 - F#m7(b5) - Gmaj7 - Am7 - Bm7
In the next article, you’ll learn how to add various extra chords to songs. However, with modal songs, you must stay within these specific chords; adding others will dilute the unique modal sound. As I mentioned in my "Guitar Scales" article, it takes time to fully grasp the sound of each mode, but composing in different modes will help you understand them much faster.
I also suggest getting a Fakebook, like the Real Book, and start improvising your own solos over jazz standards. Even if you're not a jazz player, this practice will elevate your playing to another level. I covered this in "Guitar Scales," but as a quick reminder, you can use a variety of scales over the same chord when soloing, as long as the scales contain the chord tones. For example, in a progression like Dm7 - G7 - Cmaj7, for the Dm7 chord, you could improvise using the Dorian, Dorian #4, or Dorian b2 modes. For the G7 chord, you could use the Mixolydian, Mixolydian #4, Mixolydian b6, or Mixolydian b2b6. And for the Cmaj7 chord, the Ionian, Lydian, or Lydian #2 modes are great options.
Check out that article!
HELP ME CREATE THE BEST GUITAR METHOD IN THE WORLD!
As a thank you for reading this far, I’m excited to introduce my latest release, Book of Chords. This book shows you how to take the chord concepts from this website (Triads, Drop-2 chords, Drop-3 chords, Shell Chords & Extensions, Triads & Extensions, Arranging Songs) and use them to create new voicings, arrange songs, build fresh lines for your solos, and expand your rhythmic vocabulary. The original price was $50, but I’ve lowered it to make it easier for more people to grab a copy.
All I ask in return is a little feedback. Let me know what you think—whether anything was tricky to understand, if there’s something I should add, or if you’ve got any other thoughts. I update my books all the time, and you’ll get every new version with everyone’s suggestions. Hopefully, one day this site will be a full platform for guitar theory courses with your help!
Shoot me your questions or thoughts at info@guitartheorylessons.com, and I’ll get back to you in a few days.
Digital Download
PDF Sheet Music + TAB (228 pages)
This book uses the Triads & Extensions topic to demonstrate all the exercises, but the concepts can be applied just as effectively to Triads, Drop-2, Drop-3, Shell Chords, Extensions, and even song arrangements.
What's Included?
Instructions
Appendix of Triads & Extensions
Harmonizing (Creating interesting voicings to comp and arrange)
Arpeggios Drills (Economic picking exercises + Creating new arpeggios using different voicings)
Chromatic Approaches (Bebop style technique)
Rhythmic Vocabulary
All types of triads with extensions in all 12 keys!
Triads included:
major triads
minor triads
major triads w/ dominant function
diminished triads
suspended 4th triads
augmented triads
Lydian triads
augmented triads w/ dominant function
Lydian triads w/ dominant function
Extensions included:
Or if you're looking for something simpler, you can find the Appendix of Triads & Extensions, Intervals, Drop-2, Drop-3 chords, Shell Chords & Extensions, and Scales & Modes, in the STORE section.
All of these theory concepts are available for free on my blog to anyone interested in learning more about music. However, producing this content is time-consuming, so if you found this article helpful, please leave a comment and hit the like button at the bottom of this page! Thank you for everything!
All my best,
Rodrigo Moreira